:n ならば 面積比は、m2:n2 である。 ② 相似な立体の表面積比は、相似比の2乗に等しい。 相似比がm:相似な空間図形の相似比と面積比,体積比の関係を知り, 使うことができる。 問題 の図ような円錐容器に コップ1杯の水を入れたら, 深さが容器の半分になった。 この容器を満水にするにはあ と何杯必要ですか。 文字を用いて一般的に相 似比と面積まず相似比を求める A:B=8 10=4 5 A:B=42:52 =16:25 (2) Aの表面積が240cm のときBの 表面積を求めよ。 2 16:25 A B 表面積比 = A B 240:x 実際 の値 16 16 1 15 x=375 (3) AとBの体積比を求めよ。 次に表面積比を求める A:B=4 :5 A:B=4 3:5 =64:125 相似比 体積比
求不规则四边形的面积 给出的条件似乎没什么用 关键是求相似比 生活资讯 娱乐新闻网
相似 面積比 平行四辺形
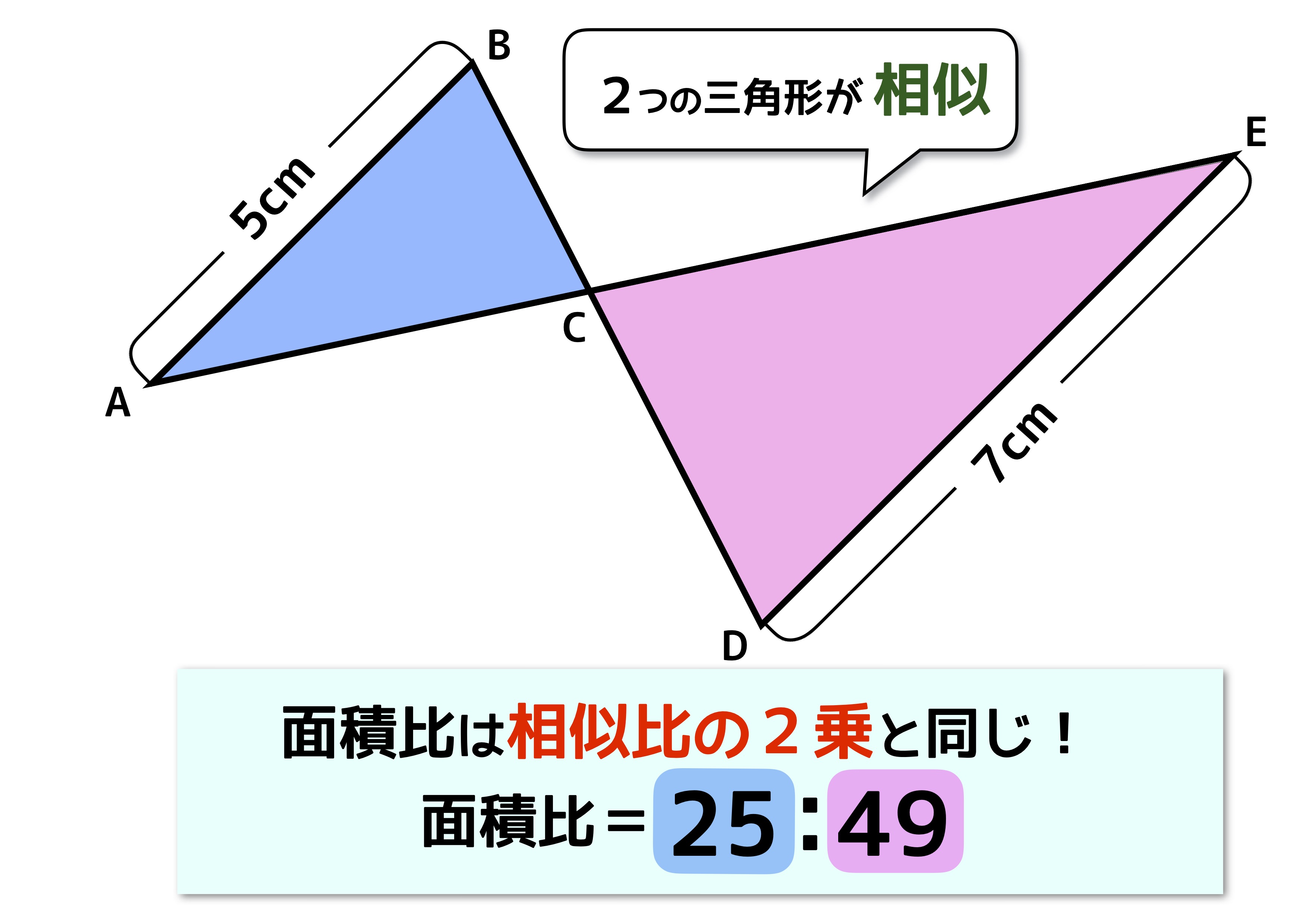
相似 面積比 平行四辺形-影片:例題相似三角形面積的比,數學 > 國中 > 九年級 > 均一版 > 相似形 > 相似三角形的應用。源自於:均一教育平台 願 每個孩子都成為終身學習者,成就自己的未來。 面積比と相似:図形の面積比は相似比の2乗 相似の図形の面積比は相似比の2乗 三角形が相似の場合、 面積比は相似比の2乗 と同じ 面積比は高さの等しい三角形の組を探す!相似は2乗!① (上記記事にも書いてあります)




九年级数学上册1 3 相似三角形练习题8 新版 青岛版 新版 青岛版初中九年级上册数学试题下载 Word模板 爱问共享资料
エ 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解す ること。 オ 相似な図形の性質を具体的な場面で活用すること。 本単元における本質的な問い ・ 2つの三角形が相似であるためには,どのような条件が相似比は底辺の比であり、高さの比でもあるため、 面積比は相似比の二乗 で求められます。 下の図では、三角形アとイの2つの辺の長さがわかっていて、その2辺に挟まれた角が同じ大きさです。故に相似な三角形の辺の比は等しくadde=fbbe=13 be=6よりfb=2 線分aeが円oの直径なので、弧aeに対する円周角より∠abe=90°より fbeは直角三角形。 ∴ fbe= 1/2 * fb * be = 6 1 後半 次に fbe gfb = fe fg 2 (fefgが分かれば面積比から gfbの面積を計算できそう・・・)
相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき五角形についても、相似比が1: k であるとき、面積の比は1: k 2 が成り立つことを確認する。 教科書130ページの問1を考える。 ※グループのメンバーで互いに、自分の考えを説明し合う活動を入れてもよい。 自分の考えを発表し、答えを確認する。⑦相似比と面積比の関係を利用して, 相似な平面図形の面積を求めるこ とができるようにさせる。 相似な平面図形の相似比と 面積比の関係を調べ,平面図 形の周や面積を相似比を利 用して求める。 2 討論・協同 相似な立体の表 面積や体積の比 ⑧
相似が言えれば apae の比がわかると面積比もわかる。 apae がわかってもそれでそのまま 2 乗が面積比になるわけではない。 相似がいえて初めて辺の比の 2 乗が面積比になるのでまずは相似を言うこ相似・線分比と面積比 レベルaの25題 問1 右の図でabとcdが平行なとき、ア〜エの長さを求めなさい。 問2 右の図でabとcdが平行なとき、ア、イ、ウの長さを求めなさい。 問3 右の図形はある土地の1:00の縮図です。この土地の実際の面積が何m2図形の相似 目次 > 相似な図形の面積比は、相似比の2乗になります。理由を考えてみましょう。例題1 abc と ABC の相似比が m:n のとき、 abc: ABC=m2:n2 であることを証明してください。 L、H を




高校入試対策数学 面積比に関する対策問題 Pikuu
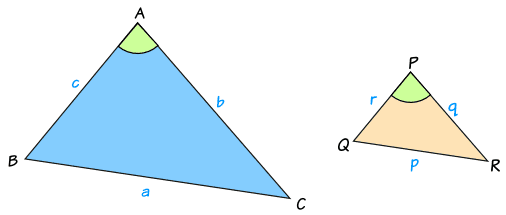



相似三角形定理
6 相似比と面積比の関係についてま 解することめる。 相似な三角形で m となる 7 シートの問1、問2を解く。 気 Qの結果から言えることを、シートに書かせた 相似な図形の相似比と面積比、それらの関係について理 とができる。<観察・学習シート>相似比と面積比についての練習です。かなり基本的な話です。 苦手な人向けです。 次回追加分は面積について計算していくものになります。 17年9月12日 画像にあるような三角形の相似に関しての長さを求める問題です。 相似比から面積比をだす 相似比が出ちゃえばあとは簡単。 相似比を2乗すれば面積比がでるってわけ。 abcと a'b'c'の相似比は、 1 2 だったね?? 面積比は2乗してやった比の、 1² 2² = 1 4 になるはず! おめでとう! 相似比から面積比を計算でき




Yip S Math 中三 相似圖形面積比及邊長比 同高 底 D面積比 Facebook




基礎 相似三角形的周長比與面積比 數學 均一教育平台
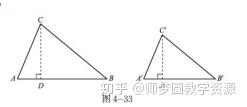
也就是兩個相似三角形中,面積的比等於對應邊長的平方比。 試著利用這個概念來解題目吧! 例題一:如下圖,平行四邊形abcd 中,e 為 ad 上一點且 ae = 2 3 ad , be 與 ac 交於f 點,求 (1) aef 面積: cbf 面積=? (2)若平行四邊形abcd 面積=30,則 aef 面積=? 相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa2:b2になる という性質があります。 これがおぼえるべき、2つ目の型です。 さきほど示した17種類の内、14個は①と②をベースにしたものです。苦手の克服 相似2 Tweet 図形の練習問題 | 16年08月日18時00分 「第301回 苦手の克服 相似2」 今回も、相似を中心とした、「辺の比と面積比」について、 苦手の克服を考えていこうと思います。 前回同様、 「相似が2組ある問題」「相似とそれ以外の



相似な図形の面積比 問題 On Vimeo
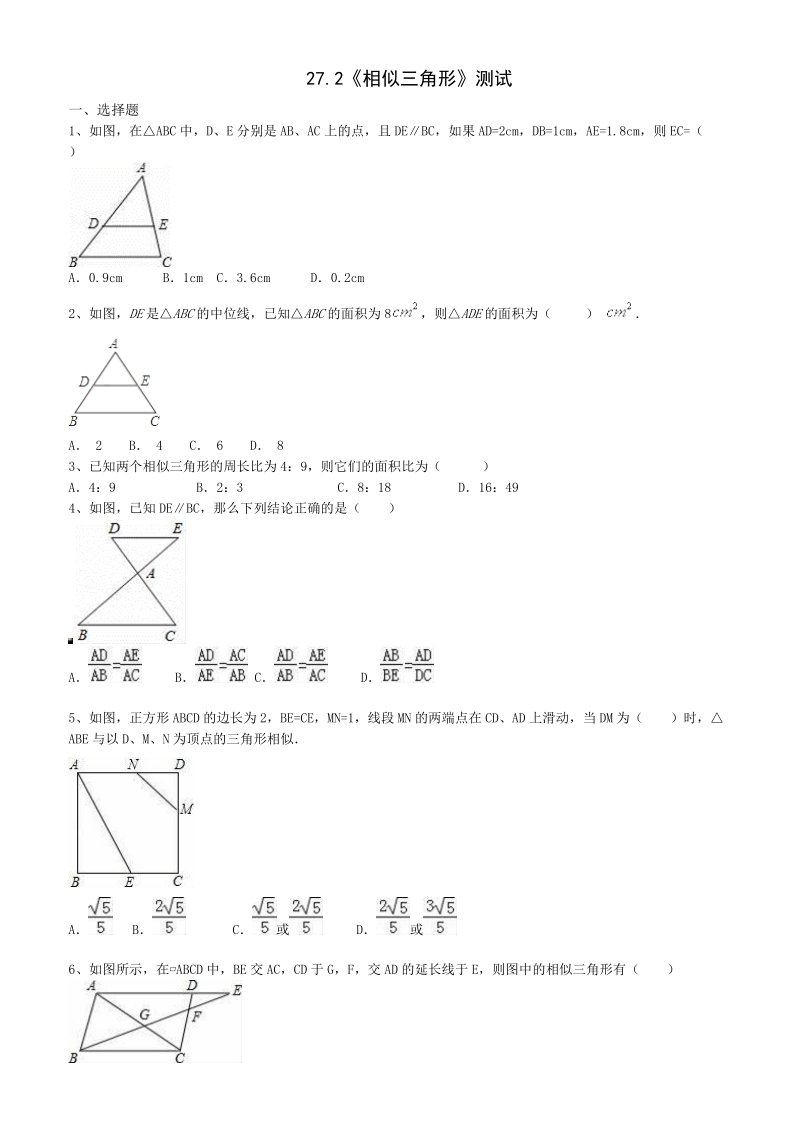



人教版数学九年级下册 27 2相似三角形 同步测试 含答案 七七文库www 77wenku Com
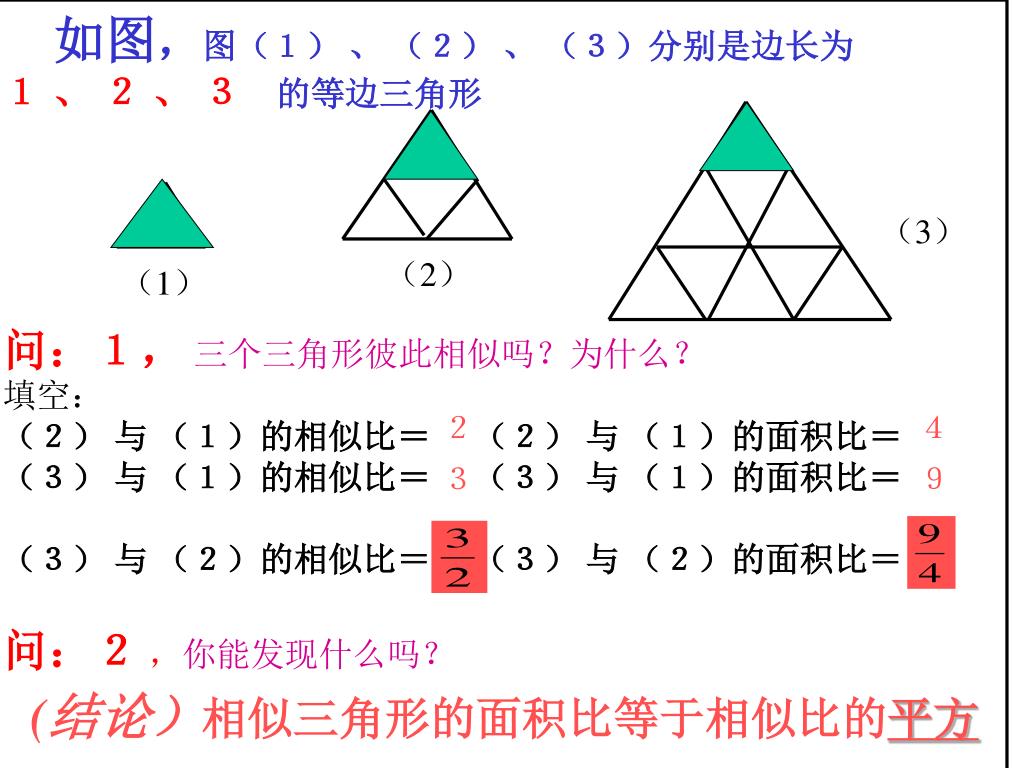
長さの比は相似比と同じ。 面積比は相似比の2乗になる。 相似比がabの相似な図形の場合 辺、高さ、周など 長さの比は a b 面積比は a 2 b 2 例 ABC∽ PQRで相似比35である。 3h 3k 5k 5h A B C P Q R ABCの高さを3hとすると PQRの高さは5hとなる。若兩個三角形相似,則三個對應角相等。 =, =, = 若2個三角形相似,則三個對應邊長成比例。除此之外,兩三角形對應的中線、高、角平分線、周長均成比例,面積比是相似比的平方。つまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも 相似な図形ならば、面積比は相似比の \(2\) 乗の比が成り立ちます。 例題1 下




九年级数学上册1 3 相似三角形练习题8 新版 青岛版 新版 青岛版初中九年级上册数学试题下载 Word模板 爱问共享资料




例題 相似三角形面積比的應用 數學 均一教育平台
3相似比の練習問題(平行四辺形1) 問1.次の各問いに答えなさい。 (ア) abcd においてae:ed =2:1 で efd の面積が2 cm 2のとき (1) cfd の面積・相似比 24:36=2:3 ・面積比 22:32=4:9 ・Lサイズの値段をx 円 4:9=:x 今日は,この相似比や面積比が日常生活のどんなところで 役に立つのか考えましょう。 次の問題に取り組みましょう。 あるピザ屋では,ミックスピザの値段が,相似比と面積の比をワークシート no1 の表に書き込ませ,相似比を1:kとして 面積の比を一般化して考えさせる。 生徒の発表を基に,相似比が1:kであ るとき,面積の比は1:k2 となることを導 き出し,確認する。 深 め る




相似三角形面积比下载 Ppt模板 爱问共享资料



2
相似比について 対応する部分の辺と角について ここでも三角形を例に話を進めてきましたが、四角形や五角形のような多角形でも同じことがいえます。 面積比 さて、相似比がわかれば、なんと面積比まで分かってしまうのです。




两个相似五边形的相似比为23则它们的面积比为 初中三年级上学期数学



这个数学核心考点 每年中考都会考 破解方法送给你



腾讯视频
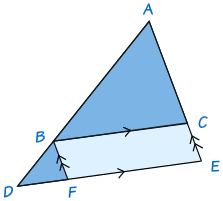



相似三角形定理




相似三角形面积比



相似三角形面积比和相似比关系 圆周角定理是什么 结论牢记 腾讯视频




相似三角形面积公式



相似三角形的问题 图片欣赏中心 急不急图文 Jpjww Com




相似三角形面积比和边长比的关系 解历史




九年级数学下册相似三角形的周长与面积专题训练 题目较难 收藏 中考 四边形 网易订阅




19 学年苏教版选修4 1 相似三角形的进一步认识课时作业 302edu教育资源网



4 4相似三角形的性质极其应用一 Ppt 沃文网wodocx Com



数学 相似三角形系列03 面积比问题



1




Ppt 相似形與sss 相似性質powerpoint Presentation Free Download Id




相似三角形面积比下载 Ppt模板 爱问共享资料



相似な図形の面積比 問題 On Vimeo




周長 面積 比 在平面幾何問題中的巧用 每日頭條



数学 相似三角形系列03 面积比问题




小升初幾何常考五大模型 等積變換 鳥頭 蝴蝶 相似 燕尾 每日頭條
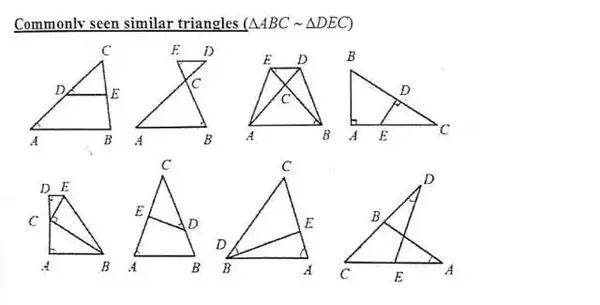



Amc 10 第三讲 运动的相似三角形 知乎




初三数学 相似三角形之 8 字模型 面积比等于相似比平方 哔哩哔哩 つロ干杯 Bilibili



相似三角形的性质 禾教 初中数学互动课堂



Ppt 18 3 相似三角形的性质powerpoint Presentation Free Download Id




巧妙利用面积比等于相似比的平方比解题 哔哩哔哩 Bilibili




翻轉學習影片 國中 數學 試題解析 102試辦會考 選擇題第21題 相似三角形面積比與柱體的體積



北师大版初中数学九年级上册相似三角形的周长比与面积比公开课优质课课件教案视频 知乎



腾讯视频



三角形的性质 万图壁纸网



动点产生的面积问题




小学阶段三角形问题五大模型 实题实练 每日头条
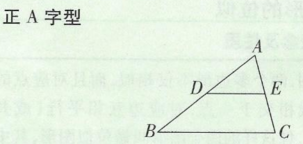



北京中考 四边形综合知识和思路 知乎




相似比 從數學上來說 相似指兩個圖形的形狀完全相同 其中一個圖形能通過放 百科知識中文網



相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online




相似三角形面积比和边长比的关系 教育频道 匠子生活



第四章相似形 图片欣赏中心 急不急图文 Jpjww Com



若两个相似三角形的面积之比为14 则它们的周长之比为a12b1 友邦知识网



1



前天刚考的公务员考试真题 3分钟 看看你能做对几道 三角形
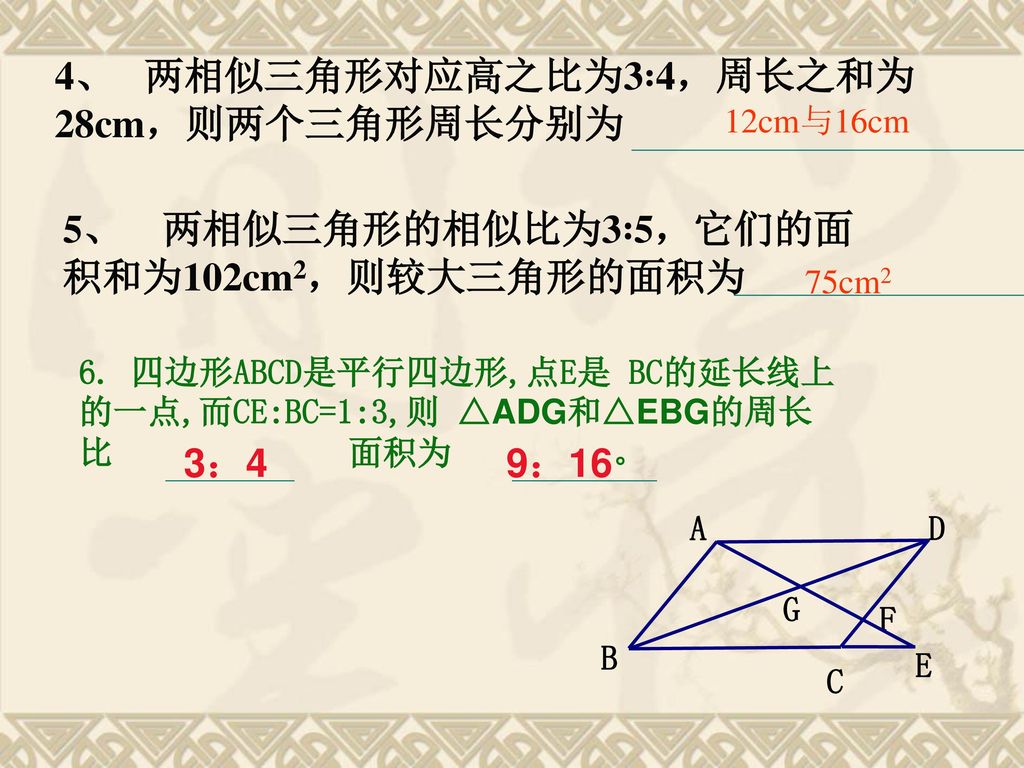



第十章图形的相似 复习课 Ppt Download




面积比等于对应边的平方比 搜索结果 哔哩哔哩 Bilibili




218几何原本第六卷 命题19 相似三角形面积的比等于相似比的平方 哔哩哔哩 つロ干杯 Bilibili




相似三角形的面積比 Isdp08am 隨意窩xuite日誌



打印预览




三角形八字模型及用法




相似じゃない三角形の面積比の求め方がよく分かりません Clear
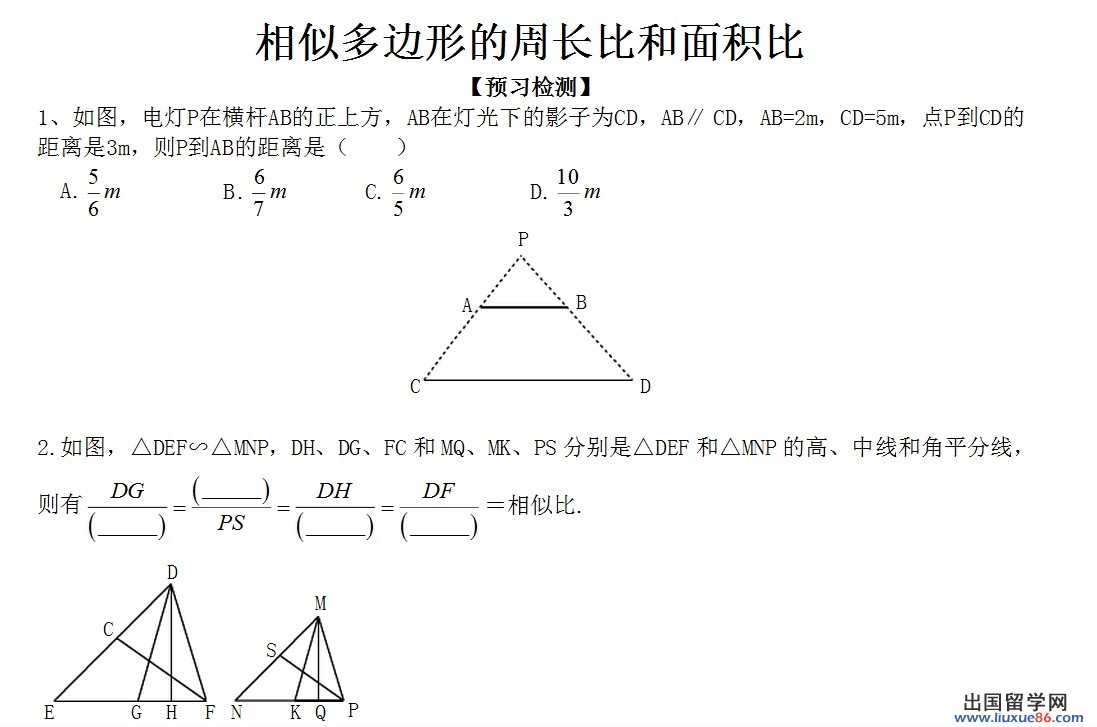



八年级下册相似多边形的周长比和面积比
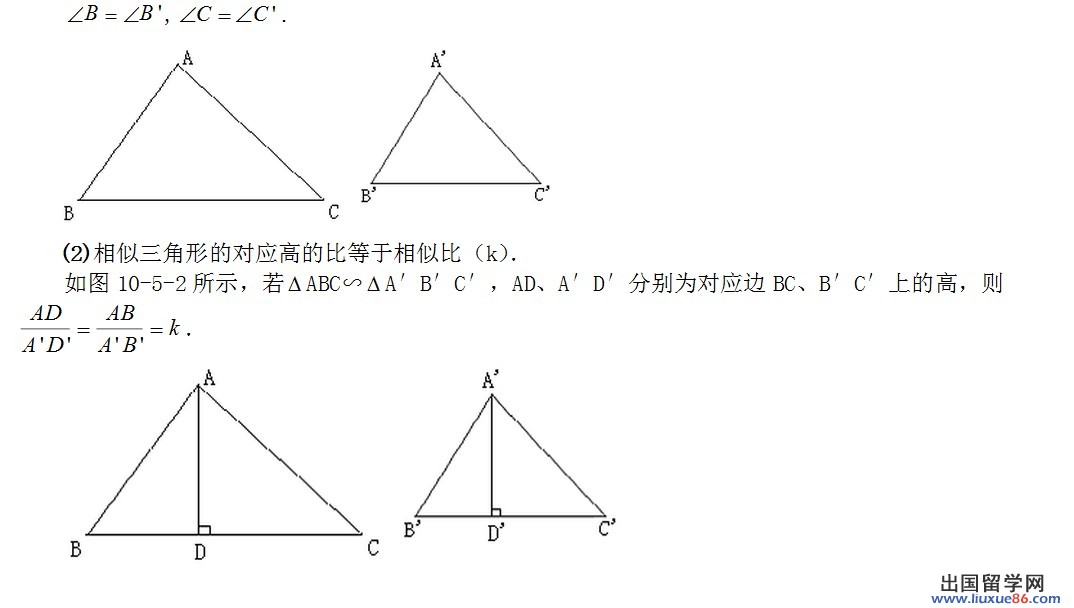



八年级下册相似多边形的周长比和面积比




两个相似三角形的面积比




朱式幸福 國中數學難題解析 3題 相似與比例




相似三角形面積比與周長比 Youtube




相似比と面積比 中学3年数学 Youtube




相似三角形面积比下载 Ppt模板 爱问共享资料



相似三角形面积比和边长比的关系 高三网



相似三角形的性质 相似ppt 第一ppt




相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online



求不规则四边形的面积 给出的条件似乎没什么用 关键是求相似比 生活资讯 娱乐新闻网



数学 相似三角形系列03 面积比问题




5 3 相似形的面积比 课本例题4 Youtube




第十章图形的相似 复习课 Ppt Download
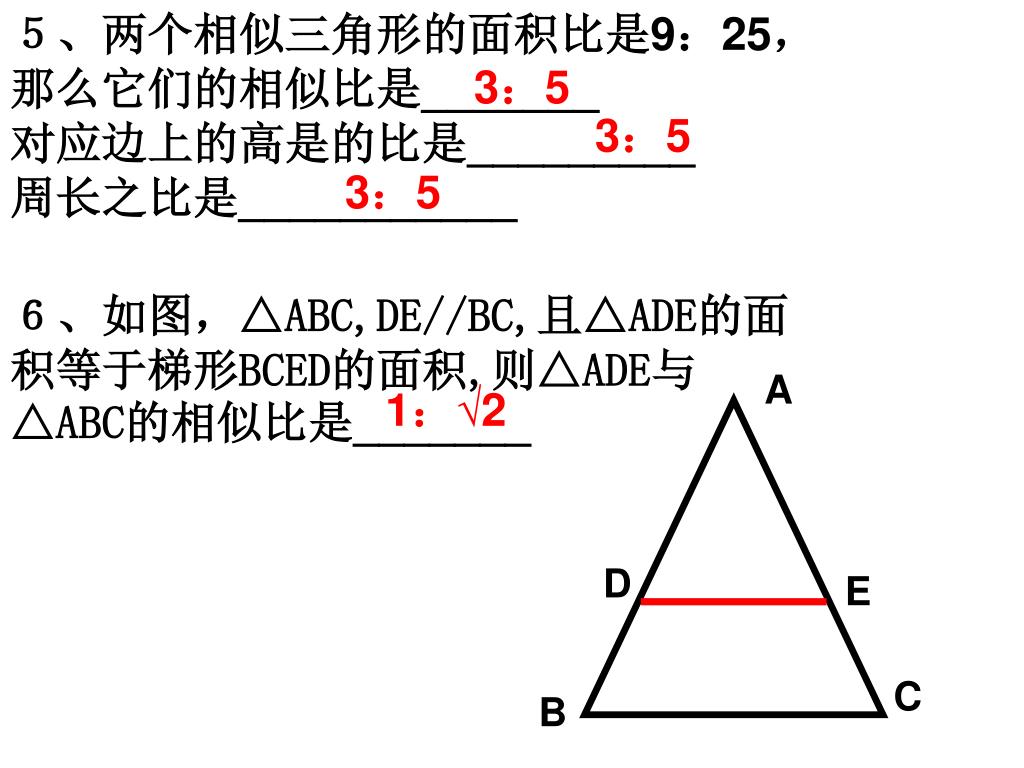



Ppt 27 2 3相似三角形的周长与面积powerpoint Presentation Id



数学 相似三角形系列03 面积比问题




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



相似三角形的面积比 初三网




相似三角形面积比下载 Ppt模板 爱问共享资料




几何原本 相似三角形面积比等于对应边的比 资讯百科全书网站




已知两个相似三角形的面积比是94则它们的相似比是其 初中三年级上学期数学




4 7相似三角形的周长和面积之比 第2课时 课件 七七文库www 77wenku Com




觀念 相似三角形的周長比與面積比 Youtube



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




李志鹏 古晋三中 分享我校数学教师林会颖老师的教学课件 指导初三学生学习相似三角形的面积比 古晋三中 线上教学



相似三角形的性质 新授课 数学错题本 微信公众号文章阅读 Wemp




相似三角形的性质及应用 知识讲解 知乎
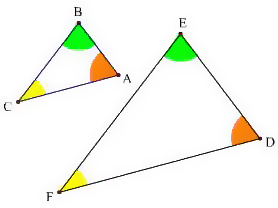



相似三角形 维基百科 自由的百科全书




九年级数学下册相似三角形的周长与面积专题训练 题目较难 收藏 中考 四边形 网易订阅



数学 相似三角形系列03 面积比问题



1




翻轉學習影片 國中 數學 相似形 等高三角形面積比



打印预览



相似三角形的性质 图形的相似ppt 第2课时 第一ppt
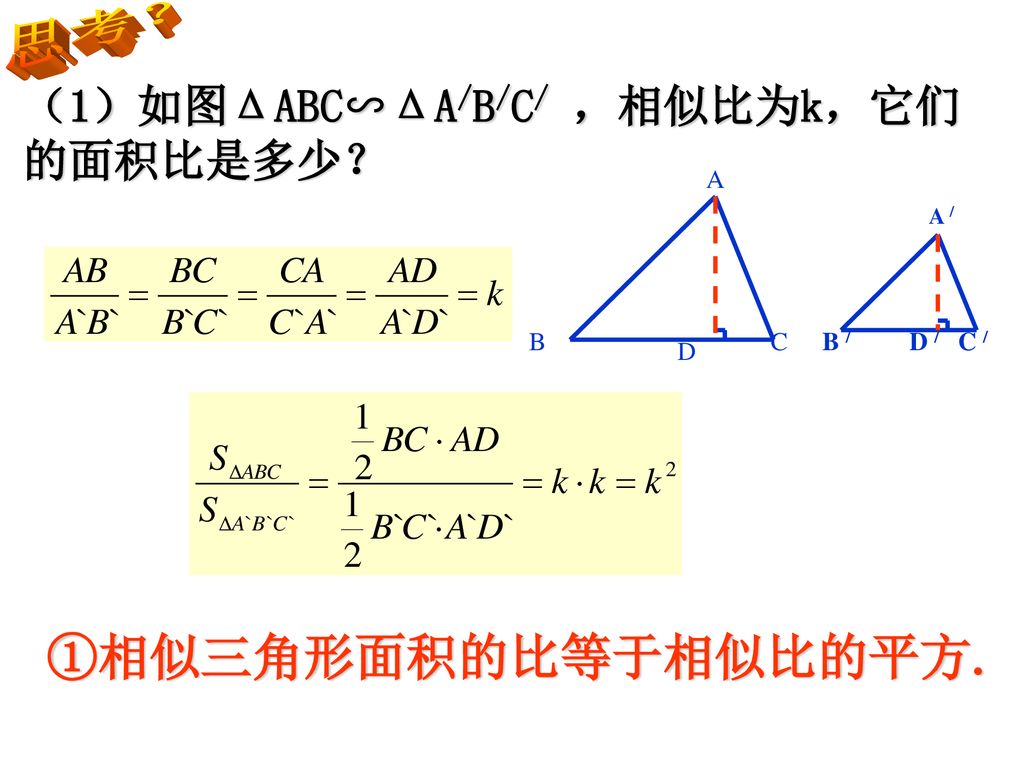



27 2 3相似三角形的周长与面积 Ppt Download




5 3相似形的面积比 练习5 2b第15题 Youtube



学霸们 来看看这几道小升初后的入学分班数学压轴几何题 爱子网



4 7 第2课时相似三角形的周长和面积之比 免费资源共享课件巴巴www Kejian Com公众号kejianbaba打包 Ppt 课件巴巴kejian Com 课件巴巴kejian Com




相似三角形面积比下载 Ppt模板 爱问共享资料



面积比例与相似 禾教 初中数学互动课堂




相似形面积比



相似三角形的面积 腾讯视频




相似三角形定理的证明



相似三角形复习课 腾讯视频



什么叫比例中项 为什么相似三角形的面积比等于相似比的平方 尚书坊
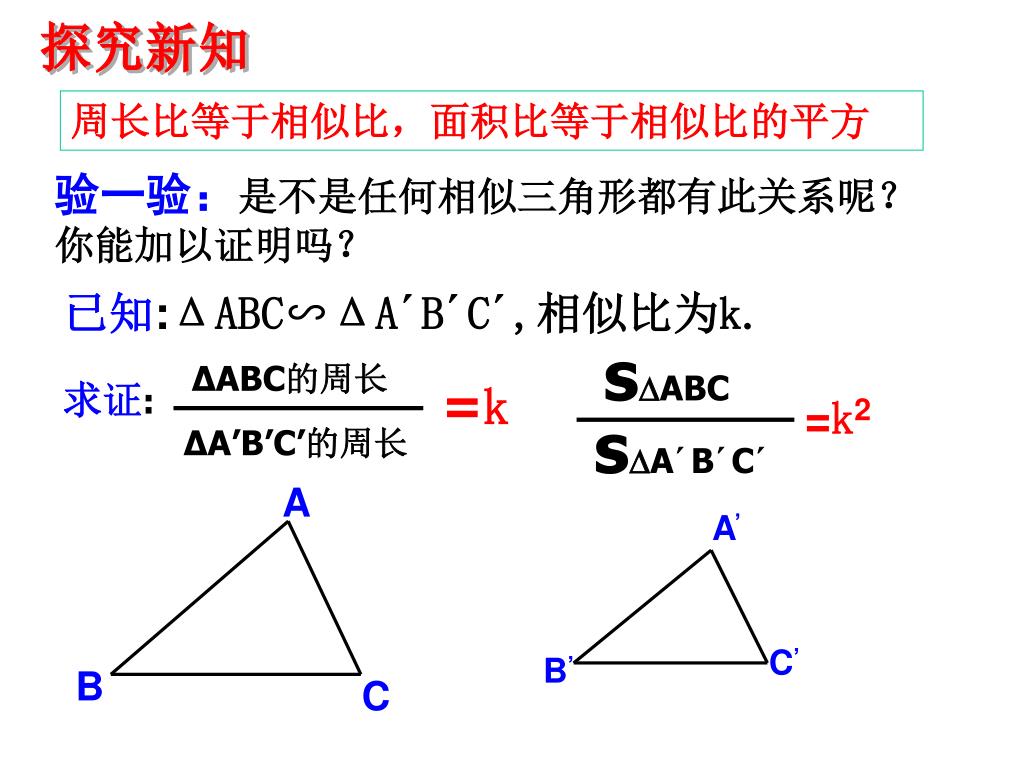



Ppt 4 4 相似三角形的性质及其应用 1 Powerpoint Presentation Id



1




Ppt 4 4 相似三角形的性质及其应用 1 Powerpoint Presentation Id



0 件のコメント:
コメントを投稿