200以上 連続する整数の和 2021 349501-連続する整数の和 2021

整数を連続した整数の和として表すことを考える。 たとえば18は、 18=567 =3456 と2通りに表される。 整数60をこのように連続した正整数の和で表すとき 互いに素な自然数の性質とその証明 スポンサーリンク 高校数学A 整数 検索用コード 連続する2つの自然数が互いに素であることを示せ \\ 8zh \hspace {5zw} (2)\ \ 連続する2つの正の奇数が互いに素であることを示せ 互いに素な自然数の性質とその当サイト「なかけんの数学ノート」は、数学の過去問の解き方や数学の考え方を解説していくサイトです。 目次 過去問 高校入試 東京都 公立高校 大学入試 共通 センター試験 数学I・数学A / センター試験 数学II・数

連続n整数の積は何の倍数 数学の偏差値を上げて合格を目指す

連続する整数の和 2021

連続する整数の和 2021-方程式文章題(整数の問題) 例題 (例1)連続する3つの奇数があり、その和は39である。この3つの奇数を求めよ。 奇数は1, 3, 5, 7, 9, と2ずつ大きくなるので 最小の数をxとすると、次はx2 となる。No276 連続する整数の和(1) Rust WA 6329 Byte t98slider No276 連続する整数の和(1) C14 AC 2 ms 3365 Byte __turtle0123 No276 連続する整数の和(1) C17 AC 2 ms 108 Byte __turtle0123 No276 連続する整数の和(1)

連続する3つの整数の積が6の倍数であることの証明 タロウ岩井の数学と英語 Note

最も小さい数をxとすると、つぎが(x1), その次が(x2)なので 3つの整数の和が21という関係を式にすると x (x1) (x2) = 21 これを計算して x x 1 x 2 = 21 3x = 21 1 2 3x = 18 x = 6 最も小さい数が6 で、次が7, その次が8である。 解答 式最も小さい数をxとする。 連続する3つの整数とそれらの和ということで、とりえずなんでもいいからやってみるのです。 3＋4＋5 あ、これだと和が12だ。57まで遠い。もっと大きい数字にしてみよう。 10＋11＋12 和が33。まだまだだ。 30＋31＋33 和が93。行き過ぎた。 ＋21＋22 和が63。 連続する4つの 整数をそれぞれ、m,(m1),(m2),(m3)と置く。 和が18になるので、 m (m 1) (m 2) (m 3) = 18 4m 6 = 18 4m = 12 m = 503 よって、連続する4つの 整数は、503,504,505,506 レベル2 具体的に考える (n = 4のとき)連続する4つの 整数は m (m 1) (m 2) (m 3) = 18

Nを偶数とすると、偶数のうち(奇数)×(偶数)の形で表せるものは、 必ずnを中心とした(2k＋1)個の連続する整数の和（負の数を含む）で表すことができる。 負の数の部分の和は、正の数の部分の和と相殺することができるので、 必ず連続する2つの自然数の和 この問題 ＞ 連続するn個の整数の二乗の和が18のとき、これらの整数を求めよ。 に解が実際に存在するのはかなり驚き。 以下ネタバレにつき改行。 ここから 2乗の和の公式を使ってしらみつぶしに調べた結果、 1^22^26^2=6*7*13/6=91 1^22^218^2=18*19*37/6=2109連続する2つの二けたの整数の二乗の和 学習について 今回は、「連続する2つの二けた整数の二乗の和」の性質を検討します。 もちろん、試験会場で実際に実験し、規則性を見出すというのも「なしではない」ですが、知っておくに越したことはありません。 このブログでサクッと理解してしまいましょう。 では、実際に見ていきます。 Q「連続する2つの二けた

21/1/17 整数 ★☆☆☆☆ 連続する自然数の和 問 どの数も素数の $2$ 乗を素因数にもつような $18$ 個の連続した整数は存在するか． 18/4/26 整数 数列の総和を とするとき となるので, として考えられる値の数を数えればよい 数列から選ぶ個数を とすると, となる 「 以上 以下の整数のうち 個の和」で表される整数は 以上 以下の整数 を、2個以上の連続した整数の和 で これは、素因数分解 ＝2×2×5×101を活用します。 ★連続する整数 中学受験 国語の勉強法！短文とメモで目指せ！ai

全国模試1位に学ぶ英語 令和3年度 京大英語21 分析 Sacramy

タロウ岩井の数学と英語 Noteの補足など 21年2月13日新型コロナワクチンの先行接種についての状況 Powered By Line

N 3 5n=n (n 2 5) =n { (n−1) (n1)6 } =n (n−1) (n1)6n ここで連続3整数の積 n (n−1) (n1) は6で割り切れ， 6n も6で割り切れるから， n 3 5n は6で割り切れる．（ 2, 3 は不可） n=1 のとき n 3 5n=6 だから4で割り切れない． ≪そんなに器用に変形できなければどうするの\(n\) から始まる連続自然数の和として \(S=n(n1)(n2)\cdots(nm)\) ( \(m\) は自然数 ) と設定します。 等差数列の和として処理してもよいですし、シグマ計算してもよいです。 整理すれば、 \((m1)(2nm)=2S\) という式を Get できると思います。 問題概略 ある整数を連続する 2 個以上の自然数の和で表す方法が何通りあるか考えます。たとえば 30 は「 」「 」「 」の 3 通りの方法があります。 429 は何通りの方法があるでしょうか。

中学受験 算数21時事問題の予想問題集 子どものための教育支援情報サイト スタディメンター

Imo 21の旅 問題1

 整数の問題です 整数の問題で理解出来ない物があります。 どなたか、御手伝いお願い致します (1)連続する3つの正の整数がある、1番小さな整数と1番大きな整数の積から 真ん中の整数の3倍を引くと69になる。方程式文章題(整数の問題) 方程式をたてて求めよ。 連続する2つの整数があり、その和は143である。この2つの整数を求めよ。 連続する3つの整数があり、その和は33である。この3つの整数を求めよ。 連続する3つの偶数があり、その和は72である。この表から3，5，7 のように2 個の連続する整数の和で表される整数，6 のように3 個の連続する整数の和で表される整数，10 のように4 個の連続する整数の和で表され る整数，9 のように2 個の連続する整数の和と3 個の連続する整数の和の2 種類で表 すことができる整数，4，8 のように連続する整数の和で表すことができない整数があ

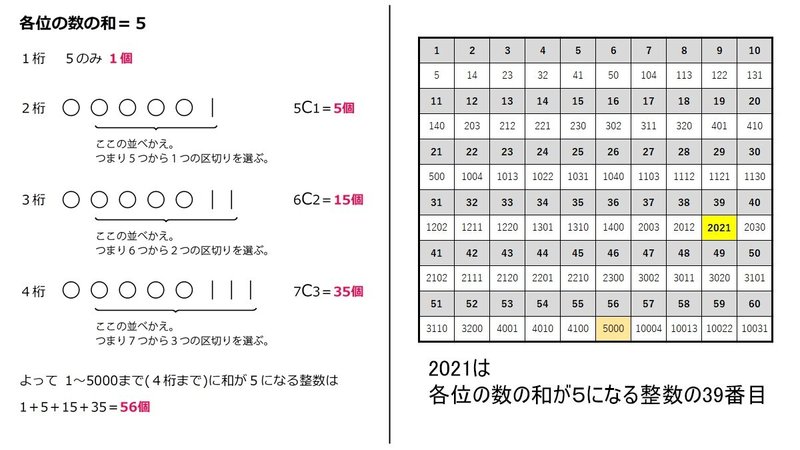
21 の数の性質まとめ みんなの算数オンライン Note

自作 数学21年問題 まとめ ほにゃらら実験室

 連続する10個の自然数の和とは、例えば とか のようなものです。上の和は55ですし、下の和は715です。 こんな計算が、あっという間にできるというのがテレビでやってたんです。 等差数列の和 普通に考えたら、これは等差数列の和です。初項を 、末項を連続する整数の和について，次の問いに答えなさい。 ① 次の文は，連続する3 つの整数の和が必ず3 の倍数になることを説明したものである。 ア ～ ウ にあてはまる式をそれぞれ答えなさい。 例えば、10＝1＋2＋3＋4のとき、個数は4で、平均は25です。 10の奇数の約数は5ですから、その半分が平均になっているということです。 よって、1以外の奇数の約数があれば、連続する整数で表すことができるということになります。 例えば、63には、1以外の奇数の約数が3、7、9、21とありますね。 63＝＋21＋22（個数が3個） 63＝6＋7＋8＋9＋10＋11＋12（個数が7

ある自然数を２個以上の連続した自然数の和で表すこと ２０１５年度横浜国立大学入試問題より 身勝手な主張

21年新春数学 パズル問題 21にまつわる性質まとめ Togetter

・連続する三つの整数の和について考える。 思連続する三つの整数の和は，いつも3の倍数になっていること を，図や式，言葉を用いて論理的に考えている。 ・連続するいくつかの整数の和につい和が n となるような，連続する2つ以上の正の整数の組み合わせは，何組存在するでしょうか？例えば， 9 は 234 と 45 の 2通りの組み合わせがあります．21は合成数であり、約数は 1, 43, 47, 21 である。 約数の和は2112。 約数の和が回文数になる54番目の数である。1つ前は1841、次は2111。(オンライン整数列大辞典の数列 a0280) 約数を4個もつ572番目の数である。1つ前は19、次は26。 21 = 43 × 47

時間単位 子の看護休暇 介護休暇の厚生労働省規定例 令和3年 21年 1月から 社会保険労務士事務所 ファインネクサス

令和3 21 年度用 中学校数学 内容解説資料a

 奇数の和が1＋3＋5＋7は下の図を用いて16と求める事が できます。この考え方を用いて1から99までの奇数の和を求めてください。 解法）一見難しいですが、冷静にやりましょう 1）1から始まる連続した奇数（1＋3＋5＋7＋9）の和＝四角数 90,30,18,6,2であるから、90を連続する自然数の和で表す方法は ①90 ② ③ ④67•••10•••1314 ⑤101•••6•••1213 ⑥(19)•••012•••2324 の6通りである ここで ⑤の場合は1＋01 ⑥の場合は＋•••問題 （奈良学園中学 10年、攻玉社中学 08年 入試問題 算数） 難易度★★★★ 1 10は、669＋770＋671 のように3個の連続する整数の和として表すことができます。次の問に答えなさい。 （1）10を4個の連続する整数の和で表すとき、この連続する 整数の中で最小の数を答えなさい。

守中日記

連続する3つの整数の積が6の倍数であることの証明 タロウ岩井の数学と英語 Note

イ 連続する3つの自然数の和は偶数である。 ウ 連続する3つの自然数の和は最も小さい数の3倍である。 エ 連続する3つの自然数の和は中央の数の3倍である。 オ 連続する3つの自然数の和は最も大きい数の3倍である。 （1） 太郎さんの説明の最後の式 3（ n 数学、化学、物理にトコトン強い理系科目専門塾です。 講師陣はこれまでも難関大学受験、国公立大学医学部医学科受験を直接指導してきた精鋭ばかりです。 もちろん、文系数学、物理基礎、化学基礎を学習したい人も大歓迎！ ！ 整数の性質連続する整数の積について ホーム 整数の性質連続する整数の積について 21年1月2日 大問5 連続する整数の和 渋幕・18開成と難関校で頻繁に出題されていた「連続する整数の和」からの出題です。 （1）は単純作業の問題。初見の受験生も、ちゃんと読めば得点できる問題。 （2）は1＋2＋3＋＋13＝91を使った問題。

自作 数学21年問題 まとめ ほにゃらら実験室

連続n整数の積は何の倍数 数学の偏差値を上げて合格を目指す

 他のΣ公式の証明は次の項で取り扱う }$ 同様に計算することで,\ 連続整数の積の和が以下のようになることがわかる 今一 1998年 東京大学 後期 理系 第3問 大学 では、21をいくつかの連続する整数の和で表すとき、最大で何個の整数の和で表すことができますか？ ヒント 21=43×47 ←これは今年の受験生が絶対に覚えていなければいけない素因数分解です。 最小の整数をA, 最大の整数をB, 連続する整数の個数をNとすると、 (A＋B)×N÷2= 21 すなわち、A＋BとNは4042の約数のペアになります。 ここで、B=A＋ (N1) よりAB= 2 実数 x x x に対して， n ≤ x < n 1 n\leq x

Newみんなの算数講座55 連続数による和分解 中学受験の算数知恵宝庫

方程式文章題 連続する整数

高校受験21 千葉県公立高校入試 数学 講評 簡単な問題を素早く正確に 時間配分がカギ リセマム

文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく

中3数学 ２次方程式の文章題２ 整数 練習編 映像授業のtry It トライイット

年12月31日と21年01月01日は33年ぶりの年越し連続素数日 Colorless Green Ideas

守中日記

3

21年新春数学 パズル問題 21にまつわる性質まとめ 5ページ目 Togetter

文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく

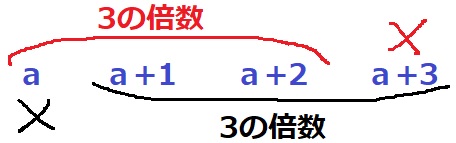
21年度 奈良県公立高校入試過去問 数学 解説 家庭教師サボの部屋

連続する4つの整数の和の性質を 文字を使って説明しなさい教えて Yahoo 知恵袋

21 西暦年数問題 数学カフェjr

高校数学b 連続する自然数の和で表せる自然数 受験の月

21 実戦 数学重要問題集 数学 Ii Iii A B 理系 内容を見る チャート式の数研出版

連続する2つの二けたの整数の二乗の和 公務員試験対策 一般知能 スペシャリストによるこっそり裏講義

連続自然数積の和 おいしい数学

自作 数学21年問題 まとめ ほにゃらら実験室

毎日やってる小テストは確実に入試につながってる 入試予想おまけ付 豊田市専門 小 中学習塾 Haruni ハルニ

連続する整数の和 さんよび 中学受験算数予備校 Note

連続する3つの整数の和が57 学習塾lily ー中学生のための高校受験専門塾ー

龍孫江の数学日誌 21年02月

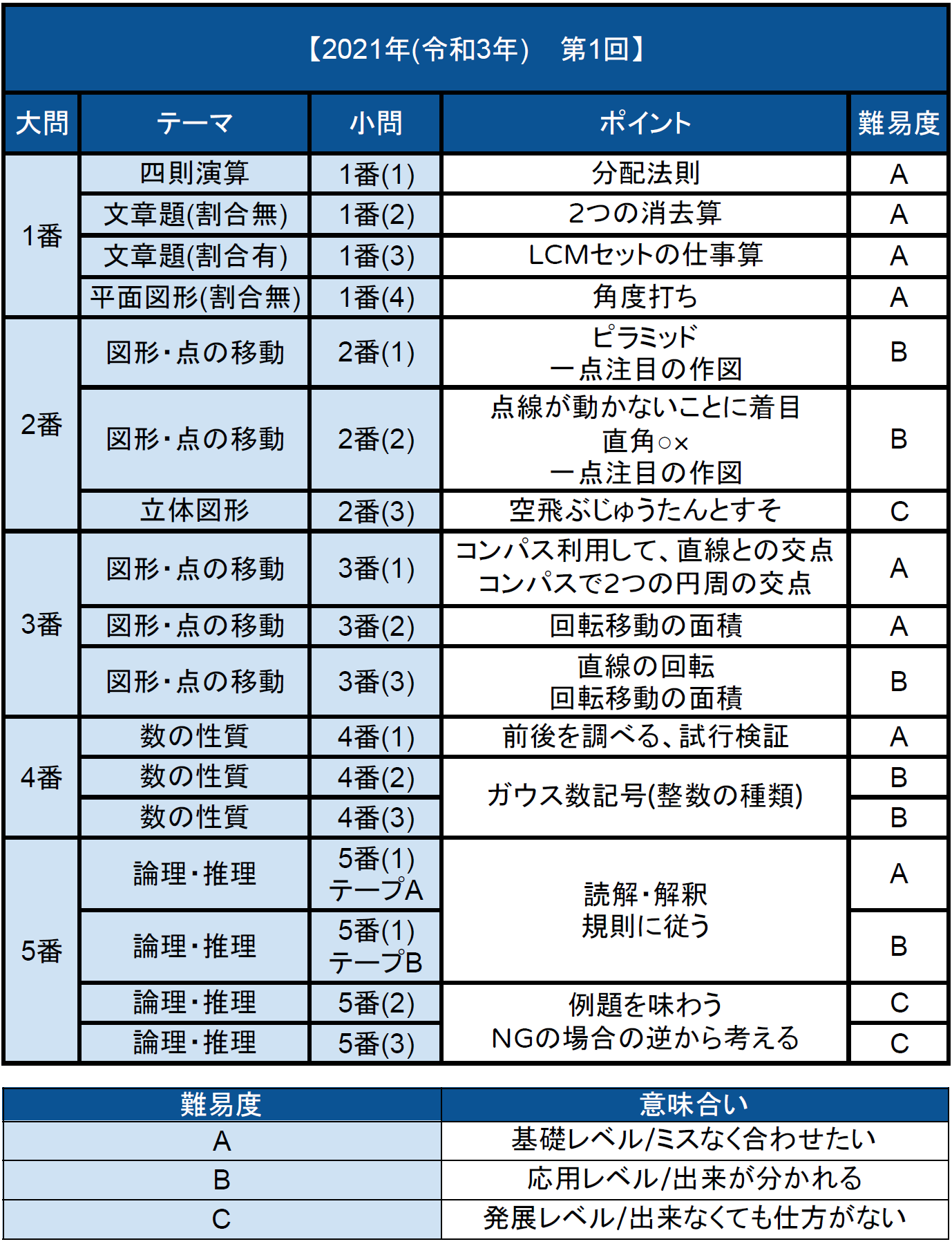
入試速報 21年市川中 算数解説動画と難易度分析 対策 中学受験コベツバ

式の計算 文字式の利用 連続する整数の和

文字を使った証明 清水塾

横浜国立大15理系第4問 連続する自然数の和を考える 偶数と奇数の積がポイント Mm参考書

黒木玄 Gen Kuroki 超算数 普通の人はリンクをたどらないのでスクショで引用 T Co Ib6utcjwth 平成年の小学校学習指導要領解説 算数編では 0を整数に含めていない 文科省は 算数科の数の範囲に関して混乱している 倍数に関して

連続整数積の和は 差の形を作って簡単に計算できる Youtube

連続する4つの整数の和の性質を 文字を使って説明しなさい教えて Yahoo 知恵袋

21年6月 Sakurai Susumu Website

令和3 21 年度用 中学校数学 内容解説資料a

Mondai78

Sacramy 大学受験総合型サイト 今週の整数問題 No 10 予習 明日でこのシリーズも第10回目となりますが 少し難しいのでまずはこちらの問題を解いてみてください 1から始まる連続する自然数の逆数の和が自然数とならない という問題です 明日は10

文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく

文字式の利用 連続する3つの整数の和が3の倍数になる証明 Youtube

21年度大学入試科目別出題分析 数学 大学受験 Y Sapix

中学数学 式による説明 のコツと練習問題

21年に出題されそうな中学入試の問題 算数編その3 Youtube

になる数式 について考えてみた Tsujimotterのノートブック

連続する３つの自然数の和 Geogebra

Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf

Newみんなの算数講座55 連続数による和分解 中学受験の算数知恵宝庫

２年生 数学 5月 21年 入野中学校 ブログ 入野中学校

高校入試問題 数学 を毎日解いてみよう 21 R3 茨城県 高校入試問題 数学 を解いてみよう

たっきー算数 Ttttaaakki Twitter

平方数の和 Pukiwiki

式の計算 文字式の利用 連続する整数の和

ワーク テスト 新しい数学 2年 東京書籍教材編集部 本 通販 Amazon

連続するn個の整数の積はn の倍数 齊藤数学教室 算数オリンピックから大学数学入門

中学入試 年号問題の難問 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法

北嶺でも 連続する整数の和で表す 22中学受験 検 指南

自然数の総和

21年 駒場東邦中 算数 問4 改 作れる整数の平均

文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく

連続する10の自然数の和はあっという間に求められるんです わたしの日常に価値はありますか

ワンダーラボ 中学入試算数 良問大賞21 Wethink

1

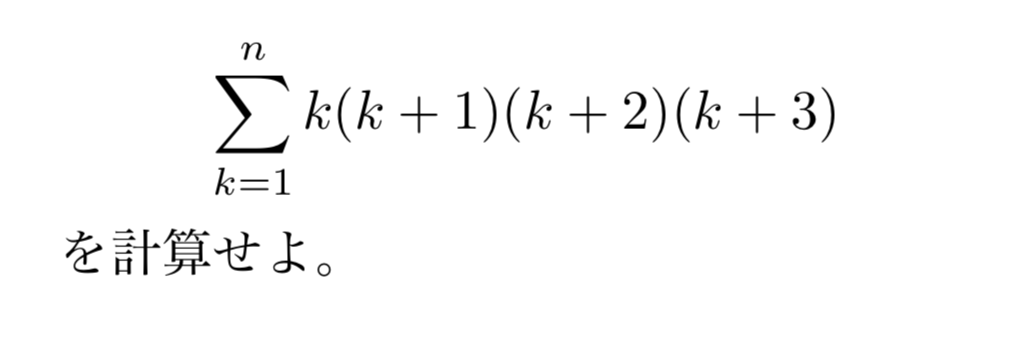
和の中抜けとは 分数や連続整数の積の総和を求める方法を例題付きで紹介 東大医学部生の相談室

入試数学演習no 18 今週の整数問題no 7 解答 解説 Sacramy

中学入試算数過去問データベース 灘中学校

中学数学 式による説明 のコツと練習問題

連続する2つの二けたの整数の二乗の和 公務員試験対策 一般知能 スペシャリストによるこっそり裏講義

文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく

高校数学ａ 整数の性質 教科書 問題 解答 公式 解説 学校よりわかりやすいサイト

21を連続した自然数の和で表す方法はから66の和 26 68の和以外に Yahoo 知恵袋

3 4 5や5 6 7のような奇数から始まる連続する3つの整数の和は6 Yahoo 知恵袋

Http Mkkc Miyazaki C Ed Jp Research Math Data H27 J Kaitou2 Pdf

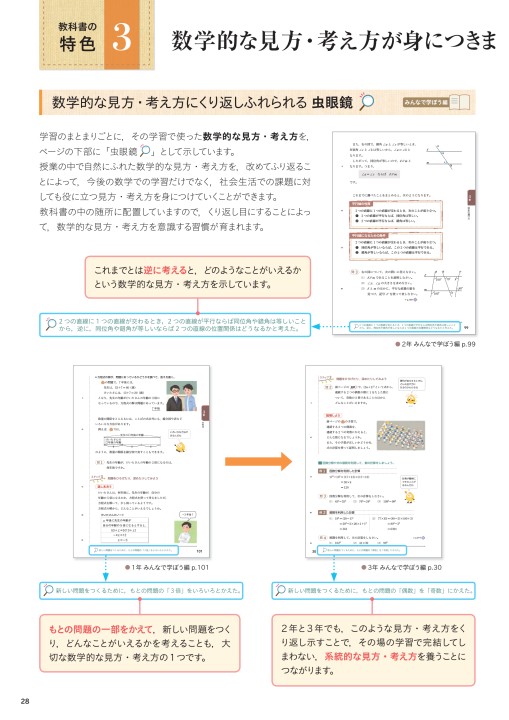
令和3 21 年度用 中学校数学 内容解説資料a

1

連続するn個の整数の積と二項係数 高校数学の美しい物語

1

ある自然数を２個以上の連続した自然数の和で表すこと ２０１５年度横浜国立大学入試問題より 身勝手な主張

素数は続くよどこまでも 年 東工大 数学 第一問 数学日和

自作 数学21年問題 まとめ ほにゃらら実験室

連続する3つの整数の和が57 学習塾lily ー中学生のための高校受験専門塾ー

21年度北嶺中学 算数 大問5 簡易解説 5 10 訂正 東京 埼玉 対面 オンライン 中学受験専門 家庭教師としのブログ

高校数学b 等差数列を利用する倍数の和 受験の月

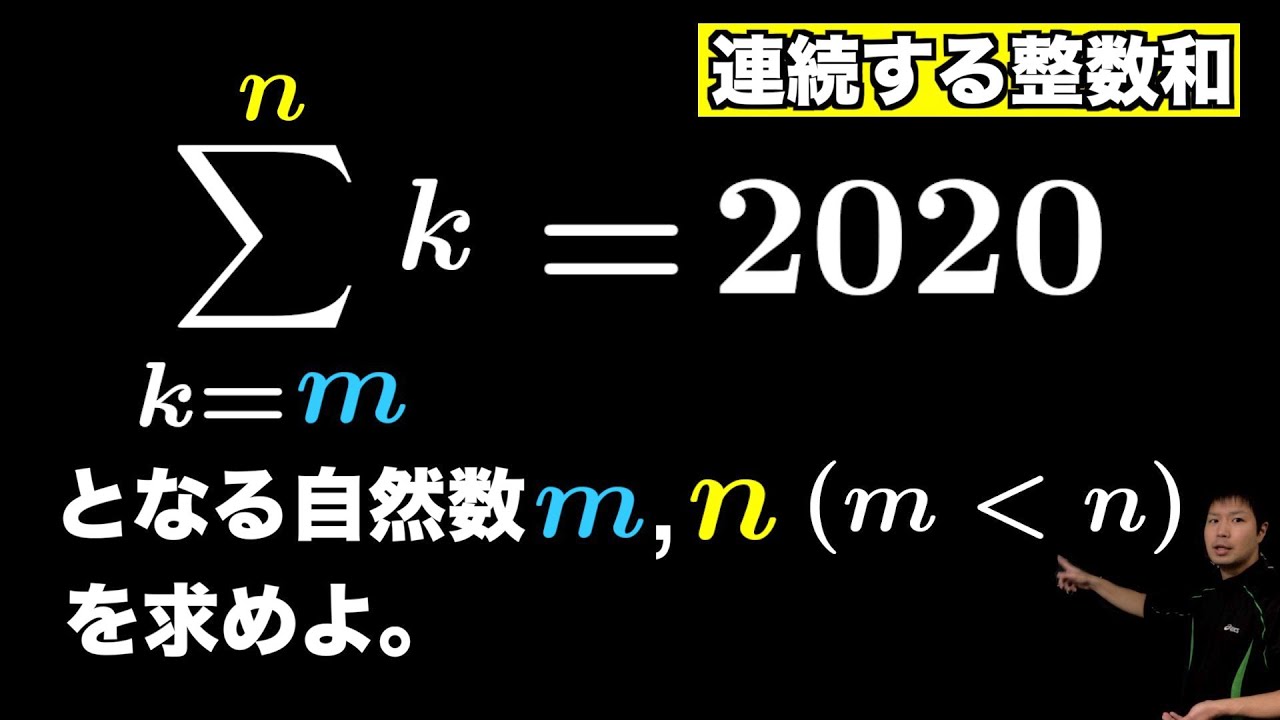
連続する自然数の和がになる場合を求めよ Youtube

2

行列 って何 どうやって計算する 行列の和 スカラー倍 積の計算を覚えよう ますますmathが好きになる 魔法の数学ノート

電気磁気工学を学ぶ 連続する3つの整数の3乗和

連続する整数の 1 乗 2 乗 3 乗の和に関する等式 Togetter

高校入試問題 数学 を毎日解いてみよう 21 奈良県

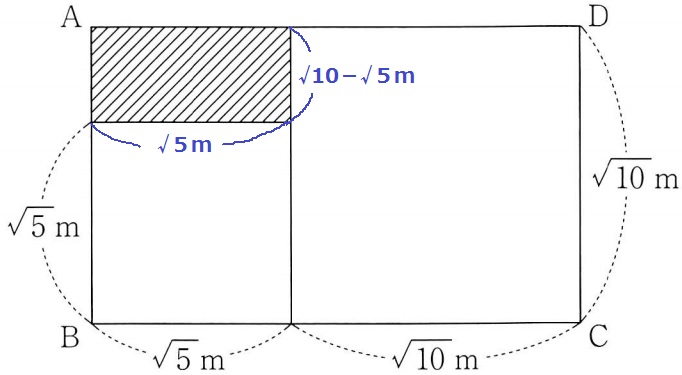
21年度 茨城県公立高校入試過去問 数学 解説 家庭教師サボの部屋

文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく

令和3 21 年度用 中学校数学 内容解説資料a

連続する4つの整数の和の性質を 文字を使って説明しなさい教えて Yahoo 知恵袋

記事 詳細情報 21年 5月 11日 火曜日 ２年生 考え方は一つじゃない 連続する３つの整数の和が３の倍数になることを証明するには ほぼ全員 最初の整数をｎとして考えをまとめていました でも実は 別解 があることを知ると なるほど

高校数学b 階差を利用する和 連続整数の積の和 Sk K 1 K 2 受験の月

ある自然数を２個以上の連続した自然数の和で表すこと ２０１５年度横浜国立大学入試問題より 身勝手な主張

Incoming Term: 連続する整数の和 2021,